P3HT Structure Research

Doped poly(3-hexylthiophene-2,5-diyl) (P3HT) has drawn significant attention from material scientists for its potential as an organic conductor. However, the relationship between the structure and function of doped P3HT remains poorly understood. In this research project conducted at UCLA's Schwartz group, molecular dynamics (MD) simulations are employed to investigate the structure of doped P3HT, using various dopants and alternative counterions including BF4¯, 2,3,5,6-Tetrafluoro-7,7,8,8-tetracyanoquinodimethane (F4TCNQ¯), bis(trifluoromethylsulphonyl)imide (TFSI¯), ClO4¯, and PF6¯, as well as different polymorphs of the doped polymer. By comparing the simulation results with experimental data, this research aims to find the structure of doped P3HT and how different counteranions influence this structure, consequently affecting the electrical properties of the doped material.

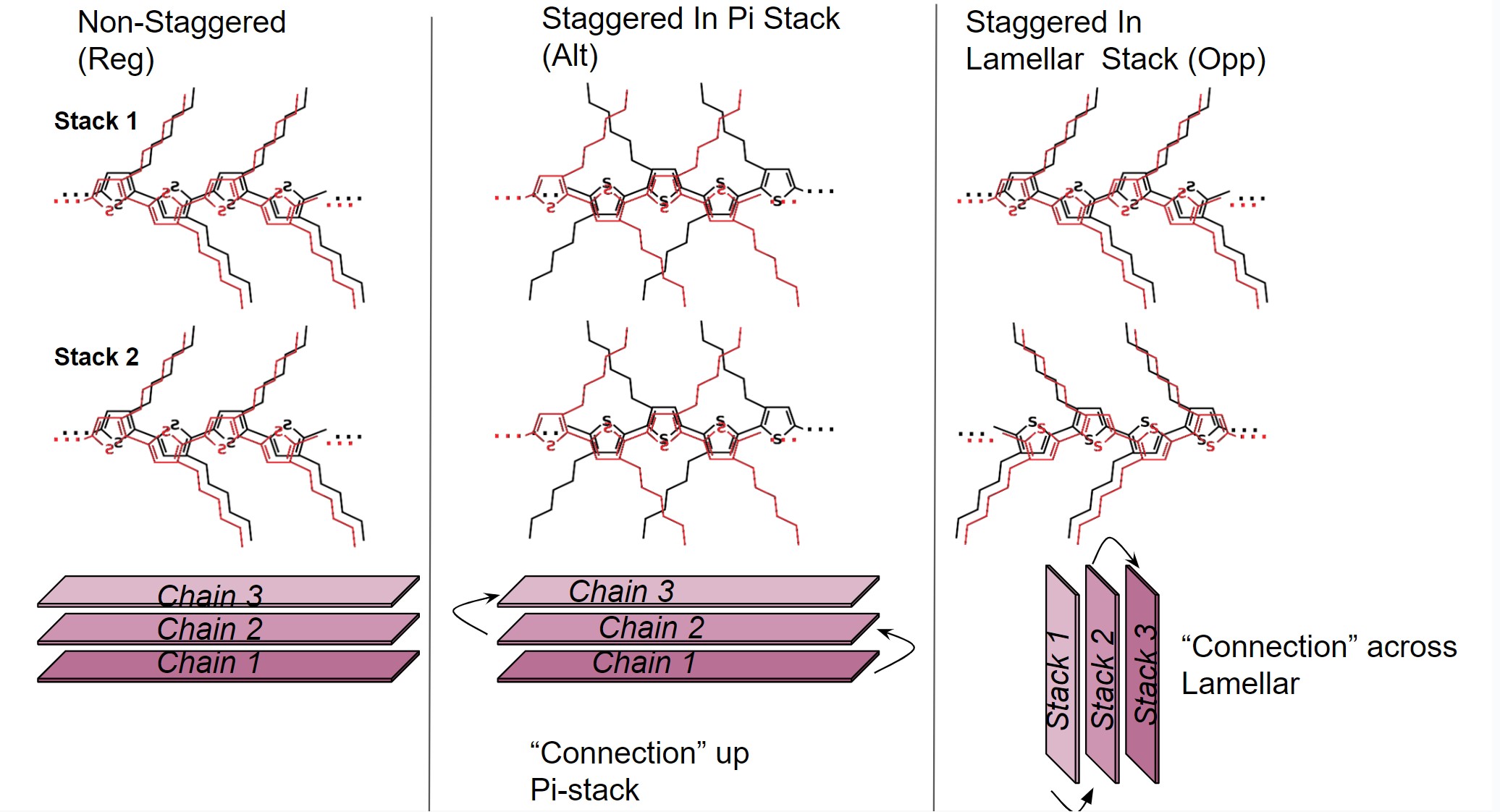
Polymorph Differences

This image provides a helpful visualization of the differences in the tested polymorphs. In the "Regular" polymorph, each P3HT chain is stacked exactly on top of each other. In the "Alternating" polymorph, each chain is flipped as you move up the polymer stack, mimicking a wrapping pattern up the stack. The "Opposite" polymorph, a different polymer stack is flipped in an opposite direction, emulating a wrapping pattern across the polymer stacks instead of upwards.

Simulation Example

This is an image of the final output of a simulation, specifically depicting the Regular Polymorph doped with PF6. From here, the simulation results can be analyzed. Each simulation contains a series of oligomers consisting of twenty-four connected monomer units in the z-direction. We then stack 12 such P3HT oligomers on top of each other in the y-direction. Finally, we repeat this structure 6 times in the x-direction, so that the total simulation consists of 72 polymer chains with 24 monomers on each chain. It is important to note that although our simulation has 72 chains, our system utilizes periodic boundary conditions, meaning that each face of our polymer rectangle “connects” at the opposite face essentially creating a quasi-infinitely large simulation cell. Approximately 50 of these simulations were run, with each simulation taking about a day to complete!